Возможно, прозрачность не кажется какой-то интересной темой. Формат GIF, позволявший некоторым пикселям просвечивать сквозь фон, опубликован более 30 лет назад. Почти в каждом приложении для графического дизайна, выпущенном за последние два десятка лет, поддерживается создание полупрозрачного контента. Эти понятия давно перестали быть чем-то новым.
В своей статье я хочу показать, что на самом деле прозрачность в цифровых изображениях намного интереснее, чем кажется — в том, что мы воспринимаем как нечто само собой разумеющееся, есть невидимая глубина и красота.
Непрозрачность
Если вам когда-нибудь доводилось смотреть сквозь розовые очки, то вы могли видеть нечто подобное тому, что показано на рисунке ниже. [В оригинале статьи многие изображения интерактивны.] Попробуйте перемещать очки, чтобы посмотреть, как они влияют на то, что сквозь них видно:

Подобные очки ALPHA-GIF работают следующим образом: они пропускают много красного цвета, приличное количество синего и совсем мало зелёного. Математику этих очков можно записать набором из трёх уравнений. Буква R обозначает результат операции, а буква D описывает точку, на которую мы смотрим. Индексы RGB обозначают красный, зелёный и синий компоненты:
RR = DR × 1.0
RG = DG × 0.7
RB = DB × 0.9
Это цветное стекло пропускает красный, зелёный и синий компоненты фона с разной силой. Иными словами, прозрачность розовых очков зависит от цвета падающего света. В общем случае прозрачность может варьироваться в зависимости от длины волны света, но в данном упрощённом примере нас интересует только то, как очки влияют на классические компоненты RGB.
Симуляция поведения обычных солнцезащитных очков гораздо проще, они обычно просто ослабляют падающий свет на какую-нибудь величину:

Эти очки пропускают только 30% проходящего через них света. Их поведение можно описать следующими уравнениями:
RR = DR × 0.3
RG = DG × 0.3
RB = DB × 0.3
Все три компонента цвета уменьшены на одинаковое значение — поглощение падающего света одинаково. Мы можем сказать, что тёмные очки на 30% прозрачны (transparent) или что они на 70% непрозрачны (opaque). Непрозрачность (Opacity) объекта определяет, сколько цвета он блокирует. В компьютерной графике мы обычно имеем дело с упрощённой моделью, в которой для описания этого свойства нужно только одно значение. Непрозрачность может пространственно варьироваться. как, например, столб дыма, который становится выше всё прозрачнее.
В реальном мире объекты с непрозрачностью 100% просто непрозрачны и они не пропускают света вообще. Мир цифровых изображений немного отличается. В нём есть пограничные случаи, когда даже сплошные непрозрачные предметы пропускают определённое количество света.
Покрытие
Векторная графика имеет дело с чёткими и бесконечно точными описаниями фигур, задаваемыми при помощи точек, отрезков прямых, кривых Безье и других математических примитивов. Когда нужно выводить фигуры на экран компьютера, эти безукоризненные сущности приходится растеризировать в битовую карту:
Растеризация векторной фигуры в битовую карту
Самый примитивный способ растеризации заключается в проверке того, где находится сэмпл пикселя — внутри или снаружи векторной фигуры. В показанных ниже примерах можно перетаскивать треугольник, в увеличенном виде движения будут более точными. Синий контур обозначает исходную векторную геометрию. Как видите, лесенка на краях треугольника выглядит некрасиво и сильно мерцает при перемещении геометрии:
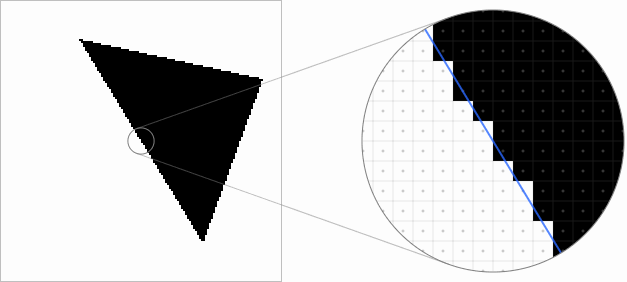
Недостаток такого подхода заключается в том, что мы выполняем только одну проверку на каждый выводимый пиксель, и результаты дискретизируются на одно из двух возможных значений — внутри или снаружи.